How to Find the area of a Trapezoid?

To find the area of a trapezoid, it is important to be able first to identify the trapezoids. Reviewing the properties of trapezoids about other quadrilaterals is useful. To make students identify trapezoids easily, they should be given pictures of different quadrilaterals and asked to identify which one are trapezoids and which one is not. 

They also need to be asked to explain their classifications and also give them examples of trapezoids in different orientations. It is recommended that you make use of the following Venn diagram to help students better grasp the concept of quadrilaterals and how they are related to one another.

(Image Courtesy: Illuminations)

Before students are taught how to find the area of a trapezoid, a warm-up exercise should take place to allow them to gauge the areas of trapezoids. Students can work in groups and make use of the Trapezoids Activity Sheet by overspreading centimeter grid paper and roughly calculate the total area in square centimeters.   Later when students calculate the actual area by using the proper measurement, they can compare their estimated figure with the accurately calculated one.

(Image Courtesy: Illuminations)

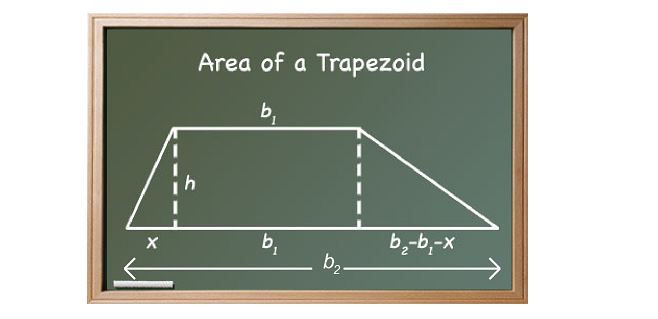
The proof of the area formula then turns out to be as follows:

The area of the rectangle is b1h. 

The area of the triangle on the left side is ½xh.

The area of the triangle on the right side

is ½(b2 – b1 – x) × h = ½b2h – ½b1h – ½xh.

The total area of the three pieces will be

b1h + ½xh + ½b2h – ½b1h – ½xh, which is further broken to ½b1h + ½b2h. This, in turn, further on becomes ½(b1 + b2) h, which is the standard area formula.

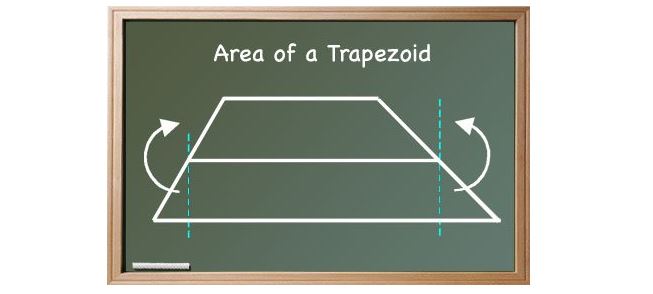
The area of a  trapezoid can also be calculated in a very different way 

(Image Courtesy: Illuminations)

If the triangles are removed from each of the corners, and then they are rotated, the subsequent diagram would be that of a rectangle. You need to keep in mind that the mid line is equal to the average of the bases. You can calculate this yourself, that is if the mid line will be equal to the base of the rectangle then once can easily calculate it using ½(b1 + b2)

You need to remember that the area of a rectangle is base height, the rectangle that is formed from the original trapezoid will have a base that would be ½(b1 + b2), and height will be h. So, the area of the rectangle and also of the trapezoid is A = ½h(b1 + b2). This is how one can find the are using the trapezoid formula. In case you are wondering as to how does the area of this new rectangle relate to the area of the trapezoid from which it was formed then you need to remember one thing. When you changed the shape of a trapezoid and turned it into a rectangle then you have only changed the shape of it, the area remains the same. 

In case you have any queries related to any maths or any other sphere of life then feel free to drop us a comment in the comment box below. 

(Featured Image Courtesy: Math Lab)