How to find Horizontal Asymptotes?

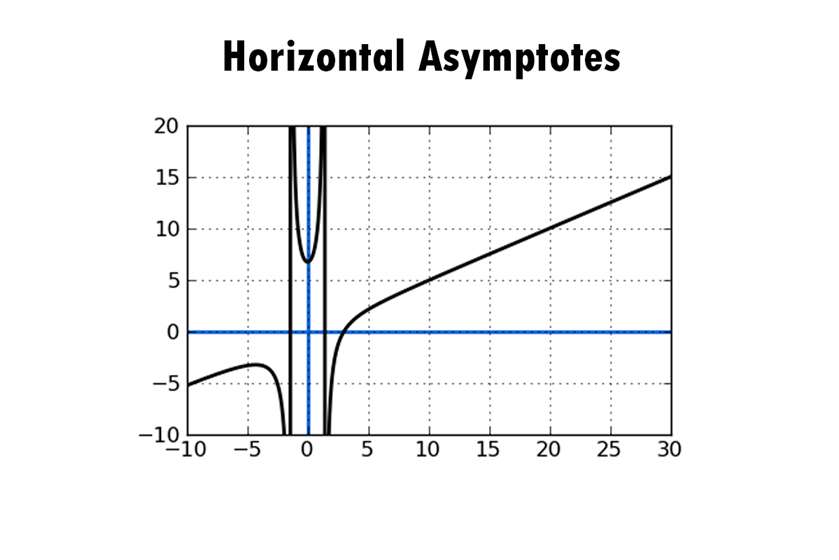
Horizontal asymptotes are completely different from vertical asymptotes. The two curves vary in a lot of ways as one can never touch vertical asymptotes, you can very well touch and cross horizontal asymptotes.

Vertical asymptotes on the graph indicate a particular behavior; they are close to the margin whereas on the contrary horizontal asymptote displays a very general behavior and are far off to the very sides of the graph.

To put it plainly, both the vertical asymptotes and horizontal asymptote are vastly different from each other. Here are few horizontal asymptote examples that better explain the concept

How to find the horizontal asymptote of the following:

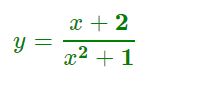
Now you would notice that the denominator is a sum of squares due to which it does not have a  factor and has no real number of zeros. So accordingly this rational function has no vertical asymptotes.

As said above, the horizontal asymptote of a function tells us where the graph would go once the 'x' increases in size. In such a case we need to look for some really big values to be assigned to 'x,' that is, values of 'x' which are way different from the origin one.

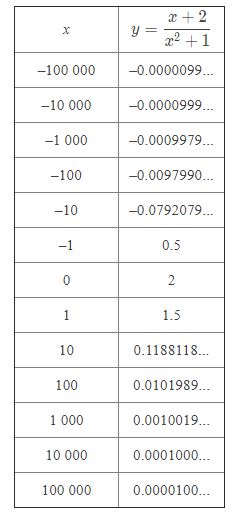
Let’s take a look at the sides of the graph where 'x' is strongly negative for, e.g., -1000 or if it is strongly positive for e.g., 10000, in this case, "+2" and the "+1" in the expression for y will not matter much at all. Since we have divided a huge number by another huge number squared, it simplified to be quite a small number.

Also notice the value of y comes from the ‘x’ and also the ‘x2’, which happened after x grew big. The x2 being the bigger number than 'x', dragged the value of the entire fraction down to y= 0 after the 'x' got big.

Maths can be a tricky topic for a lot of us and often enough problems seem to Herculean a task to overcome. We have simplified a few other mathematical concepts for you such as how to calculate the area of the circle and how to find the mean. Use the comment box below to share your feedback or any other valuable suggestion that you have.

(Featured Image Courtesy: Free Math Help)